Resources

Python program that simulates the motion of the canonball until it hits the ground and plot its trajectory

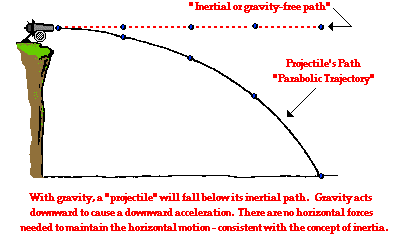
Here, we will use numerical and analytical method to plot the trajectory of the canon ball
For numerical method, we will use the simpler Euler scheme to propagate the position $x(t)$ and velocity $v(t)$ at time $t$ to $t+\Delta t$.
$x(t+\Delta t)=x(t)+v(t).\Delta t$
$v(t+\Delta t)=v(t)+\frac{F(t)}{m}.\Delta t$
Analytical Method
$x=x_0+v_0t+\frac{1}{2}at^2$
PROGRAM

#Program to simulate the motion of a canonball fired at a height of 1m above the ground
import matplotlib.pyplot as plt
v=0.0      #Initial 0 velocity
h=0.01     #dt
x=1        #Canonball is at a distance of 1m from the ground initially     
t=0.0
m=2.0
g=9.81 

ta,xa,xb=[],[],[]   #xa for numerical and xb for analytical solution

while x>=0.0:
    ta.append(t)
    xa.append(x)
    xb.append(-0.5*g*t**2.0+1)  #Analytical solution
    F=-m*g 
    x=x+v*h                      #Numerical solution #update x for the first time
    v=v+(F/m)*h
    
    t=t+h

plt.figure()

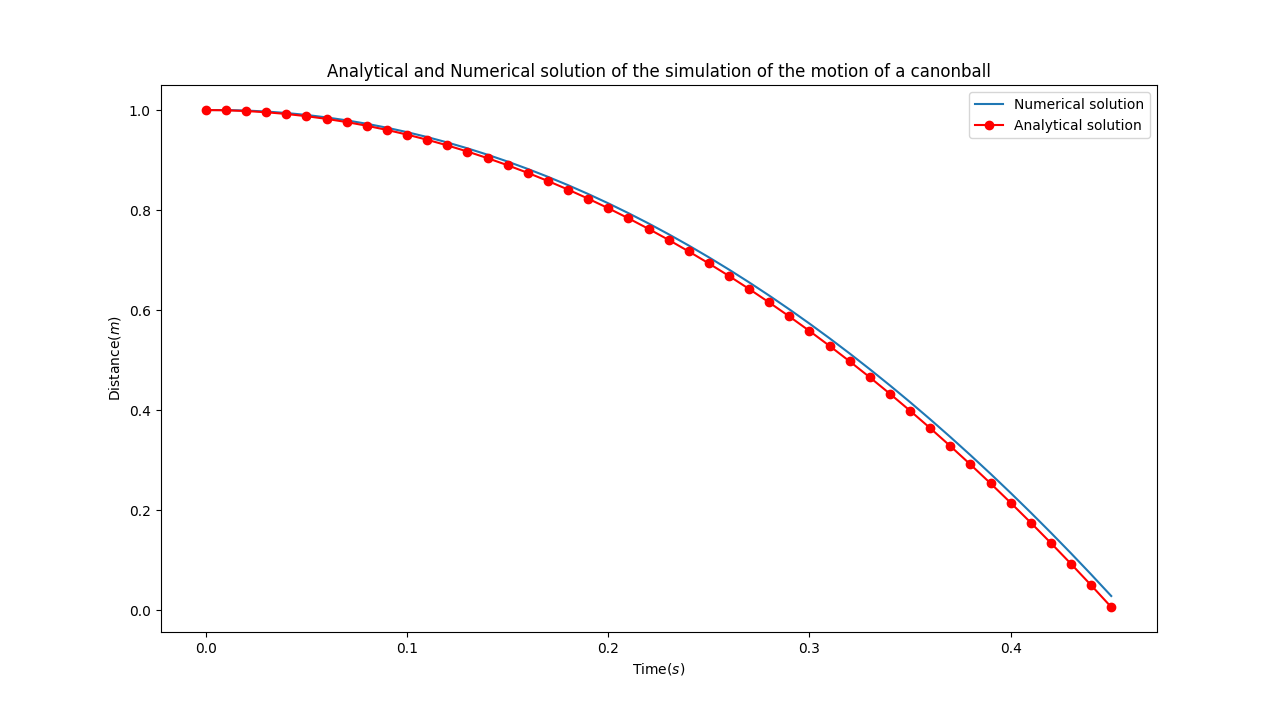
plt.title("Analytical and Numerical solution of the simulation of the motion of a canonball")
plt.plot(ta,xa,label="Numerical solution")
plt.plot(ta,xb,'ro-',label="Analytical solution")
plt.xlabel("Time($s$)")
plt.ylabel("Distance($m$)")
plt.legend()
plt.show()

PLOT